코드
# 부모 경로 구하기
def bfs(adj,s):
parent = [None for _ in adj]
parent[s] = s
level = [[s]]
while len(level[-2]) > 0:
level.append([])
for u in level[-2]:
for v in adj[u]:
if parent[v] is None:
parent[v] = u
level[-1].append(v)
return parent
# 가장 짧은 거리 경로 구하기
def unweighted_shortest_path(adj, s, t):
parent = bfs(adj,s)
if parent[t] is None:
return None
i=t
path = [t]
while i != s :
i = parent[i]
path.append(i)
return path[::-1]그래프 이론 개요
1. 그래프의 정의
- 그래프 G=(V,E)G = (V, E):
- VV는 **정점(Vertex)**들의 집합
- EE는 **간선(Edge)**들의 집합, 즉 정점들 간의 연결 관계
- 유향 그래프(Directed Graph): 간선이 방향성을 가지며, (u,v)∈E(u, v) \in E는 uu에서 vv로 가는 간선
- 무향 그래프(Undirected Graph): 간선이 방향성을 가지지 않으며, {u,v}∈E\{u, v\} \in E는 uu와 vv가 상호 연결됨
2. 그래프의 활용
그래프는 다양한 실제 문제를 모델링하는 데 사용됩니다. 대표적인 예는 다음과 같습니다.
- 네트워크 시스템: 인터넷, 컴퓨터 네트워크, 소셜 네트워크
- 경로 탐색: 도로 네트워크에서 최단 경로 찾기
- 상태 공간 탐색: 게임 상태, 퍼즐 상태 등에서 이동 가능 경로를 그래프로 표현
- 워크플로우 모델링: 작업 흐름 및 프로그램의 스펙 표현
3. 그래프의 기본 요소
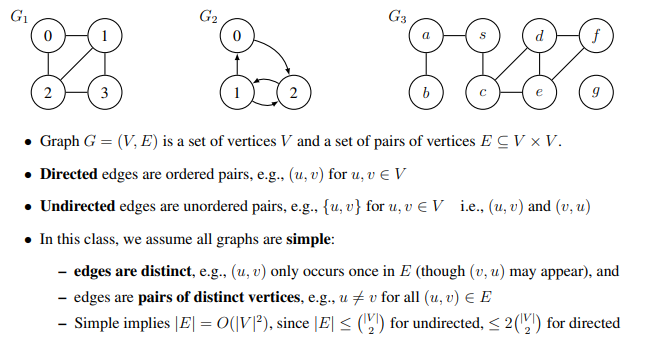
이번 수업에서는 모든 그래프가 단순하다고 가정한다.
- (u,v)는 E에서 한 번만 발생한다.(v,u)
3.1 이웃 정점 및 인접성
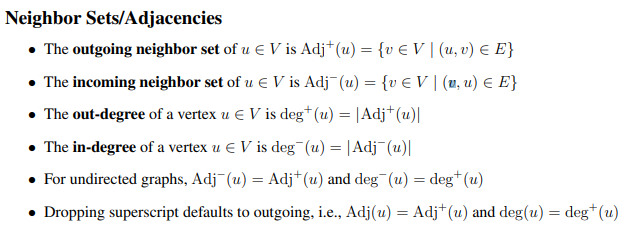
예시
- 나가는 이웃 정점(Outgoing neighbors) : 그림 G2에서 정점 1기준 0과 2이다. Adj+(1) = {0,2}
- 들어오는 이웃 정점(Incoming neighbors): 정점 1기준 2. Adj-(1) = {2}
- 차수(Degree):
- 나가는 차수(Out-degree): 정점에서 나가는 간선의 개수 / 정점 1의 out degree : 2
- 들어오는 차수(In-degree): 정점으로 들어오는 간선의 개수 / 정점 1의 in degree : 1
3.2 그래프의 표현
그래프를 저장하는 방식은 크게 두 가지로 나눌 수 있습니다.
- 인접 리스트(Adjacency List): 정점마다 그 정점과 연결된 이웃 정점들의 리스트를 저장합니다. 이 방식은 메모리 사용량이 적고, 간선의 개수가 적을 때 효율적입니다.
- 인접 행렬(Adjacency Matrix): 모든 정점 쌍에 대해 연결 여부를 행렬로 저장합니다. 이 방식은 빠른 조회가 가능하지만, 간선의 개수가 적은 희소 그래프에서는 비효율적일 수 있습니다.

4. 그래프 경로 및 문제
4.1 경로(Path)
- 경로: 정점의 순서 있는 집합 p = (v1, v2, . . . , vk) where (vi, vi+1) ∈ E for all 1 ≤ i < k.
- 단순 경로(Simple Path): 경로 상에서 정점이 반복되지 않음
- 경로의 길이: 경로를 구성하는 간선의 개수
- 최단 경로(Shortest Path): 두 정점 간의 가장 짧은 경로의 길이
4.2 그래프 경로 문제
대표적인 그래프 경로 문제는 다음과 같습니다.
- 단일 쌍 도달성(Single Pair Reachability): (G,s,t) 특정 두 정점 s, 사이에 경로가 있는지 확인
- 단일 쌍 최단 경로(Single Pair Shortest Path): (G,s,t) 두 정점 사이의 최단 경로 찾기 = 두 정점 사이 간 거리를 알 수 있음
- 단일 출발점 최단 경로(Single Source Shortest Paths): (G,s) 하나의 출발점 source에서 모든 다른 정점으로의 최단 경로 찾기
설명에서는 단일 출발점 최단 경로가 만족되면 단일 쌍 최단 경로가 만족되고 단일 쌍 도달성이 만족된다고 얘기함
5. 최단 경로 트리
- 최단 경로 트리(Shortest Path Tree)는 한 정점에서 출발해 다른 모든 정점에 도달하는 최단 경로를 포함하는 트리 구조입니다.
6. 주요 알고리즘
- BFS (너비 우선 탐색): 시작 정점에서 가까운 정점부터 탐색을 진행하는 알고리즘으로, 그래프의 모든 정점을 순차적으로 탐색하는 데 사용됩니다.
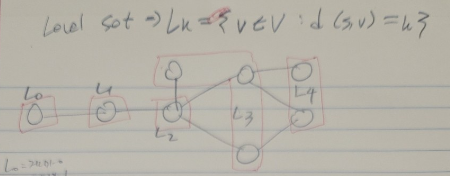
BFS와 Level 구조
BFS(Breadth-First Search)는 그래프의 모든 정점을 특정한 거리 순으로 탐색하는 알고리즘입니다. 이때 정점들은 **소스(source)**에서부터의 거리에 따라 묶입니다. 예를 들어:
- L0는 소스 정점 s 자체를 포함합니다. 즉, d(s, s) = 0인 정점들입니다.
- L1은 소스에서 1개의 간선으로 도달할 수 있는 정점들입니다. 즉, d(s, v) = 1인 모든 v가 L1에 포함됩니다.
- L2는 소스에서 2개의 간선을 거쳐 도달할 수 있는 정점들로 구성됩니다. 즉, d(s, v) = 2인 정점들이 포함됩니다.
- 이런 방식으로 계속해서 Ln까지 이어집니다.
이 구조에서 각 Lk는 **직전 레벨 L(k-1)**과 **직후 레벨 L(k+1)**의 거리 정보를 포함하게 됩니다. 즉, BFS를 수행하면서, 특정 레벨의 정점을 탐색하면 그 정점에 연결된 다음 레벨의 정점들이 탐색 대상이 됩니다.
공간 복잡도 설명
BFS는 주로 **큐(queue)**를 사용하여 구현되며, 큐에는 현재 탐색 중인 레벨에 있는 정점들이 담깁니다. 각 레벨의 정점들을 탐색하면, 그 다음 레벨의 정점들이 큐에 추가되며, 한 번 탐색한 정점은 큐에서 제거됩니다.
이때 교수님이 설명하신 내용은, BFS 탐색 시 공간 복잡도가 O(V), 즉 정점 수 만큼 필요하다는 것입니다. 이는 각 레벨의 정점들이 큐에 저장되기 때문입니다. 구체적으로:
- 한 번에 탐색되는 정점은 한 레벨의 정점들이므로, 그 순간에는 최대 V개의 정점이 큐에 들어 있을 수 있습니다.
- BFS는 그래프의 모든 정점을 한 번씩만 탐색하므로, 공간 복잡도는 O(V)입니다.
즉, BFS는 한 번에 L0, L1, L2, L3, L4 등 각 레벨을 차례로 탐색하며, 각 레벨의 정점들이 큐에 저장되어 공간을 차지하게 되는 것이죠.
이 구조를 통해 BFS는 그래프 탐색을 할 때 가장 가까운 정점부터 차례로 탐색할 수 있으며, 모든 정점을 빠짐없이 탐색할 수 있습니다.
요약
- L0은 소스에서 시작하는 정점이며, 그 다음 레벨로 L1, L2 등이 이어집니다.
- 각 Lk는 소스에서의 거리가 같은 정점들로 구성됩니다.
- 공간 복잡도는 최대 **O(V)**이며, 이는 BFS에서 큐에 저장된 정점들 때문입니다.
BFS 탐색 과정은 가장 가까운 정점부터 차례대로 탐색하는 구조로, 그래프를 순서대로 효율적으로 탐색할 수 있습니다.
알고리즘 수업의 핵심 아이디어는 !! `축소` 에 대한 아이디어이다. 한 기능을 사용하여 다른 기능을 해결할 수 있다.
'SW 사관학교 정글(Jungle) > 자료구조&알고리즘' 카테고리의 다른 글
| [DP] 다이나믹 프로그래밍 피보나치 예제 (0) | 2024.10.29 |
|---|---|
| 카데인 알고리즘(kadne`s Algorithm) 연속된 부분 배열 중 최대 합 찾기 (0) | 2024.10.29 |
| 최소 신장 트리(MST, Minimum Spanning Tree) (0) | 2024.08.21 |
| 위상 정렬(Topology Sort), boj(백준) 2252번 예시 (0) | 2024.08.21 |
| [알고리즘] 셸 정렬(shell sort) (0) | 2024.08.13 |